Mbështjellja e dhuratave të Krishtlindjes me forma të çuditshme është gjithmonë një dhimbje koke, por ja formula për mbështjelljen perfekte.
I ke zgjedhur me kujdes dhuratat. Ke gati gërshërët, shiritin ngjitës dhe madje edhe disa rrotulla letre festive. Megjithatë, për shumicën prej nesh, dhurata përfundon e mbështjellë në mënyrë kaotike, me copa letre të palosura keq dhe me tepricë shiriti.
Kjo është arsyeja pse mbështjellja e dhuratave të Krishtlindjes rrallë është një punë e dashur. Por këtë vit, ndoshta do të ishte mirë t’i shtosh një vizore dhe një kalkulator pajisjeve festive. Është koha të përdorësh fuqinë e matematikës këtë Krishtlindje.
Të mendosh jashtë kutisë
Ndoshta objektet më të lehta për t’u mbështjellë janë kutitë kubike. Por edhe këtu shumë prej nesh e kanë të vështirë të presin sasinë e saktë të letrës. Ose përfundojmë me tepricë letre të palosur rrëmujshëm në skaje, ose na mungon letra dhe detyrohemi të improvizojmë.
Ekziston, megjithatë, një formulë elegante e zhvilluar nga Sara Santos, matematikane në King’s College London, e cila ndihmon jo vetëm në uljen e mbetjeve, por edhe në përputhjen e modeleve të letrës. Fillimisht mat lartësinë e kutisë dhe shumëzoje me 1.5. Më pas mat diagonalen e faqes më të madhe të kutisë nga një cep në tjetrin. Shto këto dy vlera dhe do të marrësh përmasat e katrorit të letrës që duhet të presësh.
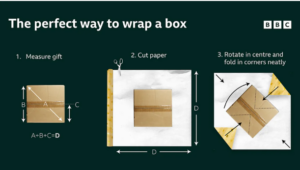
Për shembull, nëse ke një kub me diagonale 4.5 cm dhe lartësi 3 cm, duhet të presësh një katror letre 9 cm x 9 cm. Por ja pjesa më interesante…
Vendose dhuratën në qendër të letrës dhe rrotulloje në mënyrë që të qëndrojë diagonal. Pastaj sill me kujdes katër cepat e letrës drejt qendrës, duke futur palat e vogla nën palat më të mëdha. Mjaftojnë vetëm tre copa të vogla shiriti për ta fiksuar, dhe nëse letra ka vija, modeli madje mund të përputhet bukur.
Kjo metodë ndonjëherë funksionon edhe për kuti drejtkëndore. Megjithatë, siç thotë Holly Krieger, profesoreshë e matematikës në Universitetin e Kembrixhit, “nuk është gjithmonë e vërtetë që mbështjellja diagonale është më e mirë”. Për shembull, një kuti 2 x 4 x 8 cm kërkon një katror 14 x 14 cm në mënyrën diagonale, por mund të mbështillet në mënyrë tradicionale me vetëm 12 x 12 cm letër.
Truku i vendosjes diagonale është veçanërisht i dobishëm kur ke një copë letre katrore që nuk mjafton në mënyrën klasike. Duke e rrotulluar kutinë, letra mund të mbulojë dhuratën. E njëjta gjë vlen edhe për kutitë drejtkëndore, si kutitë e këpucëve.
Zgjidhje “akute”
Kjo metodë ndonjëherë funksionon edhe për prizma trekëndore. Në këtë rast, mat lartësinë e trekëndëshit në fund të paketimit, dyfishoje atë dhe shtoje me gjatësinë e kutisë. Kjo të jep gjatësinë perfekte të letrës për një mbështjellje të pastër dhe elegante.
Për dhurata cilindrike, si një tub me ëmbëlsira, mat diametrin e bazës rrethore dhe shumëzoje me Pi (3.14) për të gjetur sasinë e letrës që nevojitet për ta rrethuar. Pastaj mat gjatësinë e tubit dhe shto diametrin e një rrethi për të gjetur gjatësinë minimale të letrës. Kështu, letra do të bashkohet saktësisht në qendër të secilit skaj, duke kërkuar vetëm një copë të vogël shiriti. Gjithsesi, është mirë të lësh pak rezervë për të mos rrezikuar zbulimin e surprizës.
Rreth e rrotull
Nëse ke blerë një top, përgatitu për vështirësi – sferat janë format më të vështira për t’u mbështjellë. Është e pamundur t’i mbulosh pa rrudha, jo vetëm për shkak të vetive të letrës, por edhe për shkak të të ashtuquajturit “teorema e topit me qime”, shpjegon Sophie Maclean, studente doktorature dhe komunikuese e matematikës në King’s College London. Ajo thotë se është e pamundur të sheshohet plotësisht një sipërfaqe sferike pa krijuar të paktën një rrudhë ose fryrje.
“Nuk ka si ta mbështjellësh një top në mënyrë krejtësisht të lëmuar,” thotë Maclean. “Gjithmonë do të ketë një fryrje ose boshllëk. Personalisht, këtu do të bëhesha kreative – një fjongo, një kthesë letre, apo një formë si karamele festive.”

Nëse qëllimi yt është efikasiteti, shkencëtarë ndërkombëtarë kanë studiuar mënyrën se si mbështillen çokollatat Mozartkugel. Ata zbuluan se forma e letrës që minimizon perimetrin zvogëlon mbetjet dhe se katrori është më efikas se drejtkëndëshi. Forma me “petale” janë gjithashtu efikase, por për mbulim perfekt do të duheshin pafund petale. Zgjidhja më efikase rezultoi të ishte mbështjellja me formë trekëndëshi barabrinjës, me kursime të vogla në sipërfaqe që bëhen të rëndësishme në prodhim masiv.
Të gjithë kemi pasur vështirësi me objekte të çrregullta si filxhanët, që janë cilindra të hapur me dorezë. “Nuk ka matematikë të saktë për çdo formë të mundshme,” thotë Krieger. “Në këto raste, eksperimentimi është shpesh më i dobishëm sesa përpjekja për ta përshkruar gjithçka matematikisht.”
Një zgjidhje mund të jetë bashkimi i një dhurate të vështirë me një tjetër, për të krijuar një formë më të rregullt dhe më të lehtë për t’u mbështjellë.
Efikasitet maksimal, pa prerë qoshet
Mbështjellja e dy dhuratave me madhësi të ngjashme së bashku është më efikase sesa mbështjellja e tyre veçmas, sepse kërkon më pak letër. Por kur dhuratat kanë forma ose përmasa shumë të ndryshme, zakonisht nevojitet më shumë letër sesa për secilën më vete.
Marrë nga BBC. Përshtati në shqip Skyweb.al






















